2020. 11. 5. 22:34ㆍ전기공부/전기회로
6. 교류 전류를 페이저로 나타내기.
교류 전압, 전류는 시간에 따라 값이 계속해서 변한다.
값이 계속 변하기 때문에 두 교류를 더하거나 빼기 어렵다.
이때 이런 교류값을 페이저로 변환하면 좀 더 쉽게 계산 가능하다.
교류값을 페이저로 변환해보고, 두 교류값을 계산해보자.
1. 교류를 페이저로 표현해보기
2. 교류식을 페이저로 변환하기 예시
3. 페이저식의 더하기, 빼기, 곱하기, 나누기 예시
1. 교류를 페이저로 표현해보기
페이저란?
페이저(Phasor)는 오일러 공식을 이용해 시간에 대해 진폭, 위상, 주기가 불변인 정현함수를 표현하는 방법이다.
페이저를 이용하면 복잡한 삼각함수 연산을 복소수의 계산으로 대체할 수 있어 편리하다.
교류를 페이저로 표현해보기 전에 먼저 교류를 시간에 대한 함수로 나타내보자.
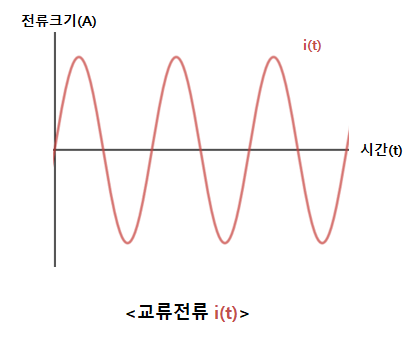
위의 교류전류을 시간에 따른 함수로 표현하면
교류전류 i(t) = Im · sin(wt + θ) 로 나타낼 수 있다.
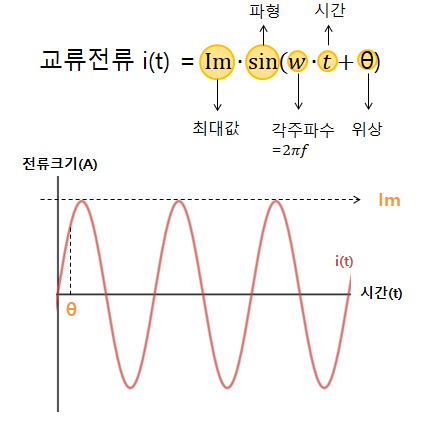
이 함수에서
Im은 교류전류 그래프에서 최대값을 말한다.
sin은 정현파중 sin파형을 말하며 cos인 경우 cos 파형이다. 사인파형이나 코사인 파형은 어느 시점에서 보느냐 관점의 차이일 뿐이지 둘 다 같은 정현파다.
w는 각주파수로 2πf와 같다. 2π는 상수이므로 f(주파수) 값변화에 따라 달라진다.
θ는 현재의 위상을 말한다.
시간에 따른 교류전류 함수를 페이저로 바꿔보자.
시간에 따른 교류전류 함수 i(t) = √2· I · sin(wt + θ)
(여기에서 I는 실효값이다. 실효값에 √2를 곱하면 최대값이므로 위에서 봤던 i(t) = Im · sin(wt + θ) 와 같다.)
이 함수를 페이저로 표현하기 위해서는 위의 교류전류 함수 i(t)를 복소평면으로 가지고 와야한다.
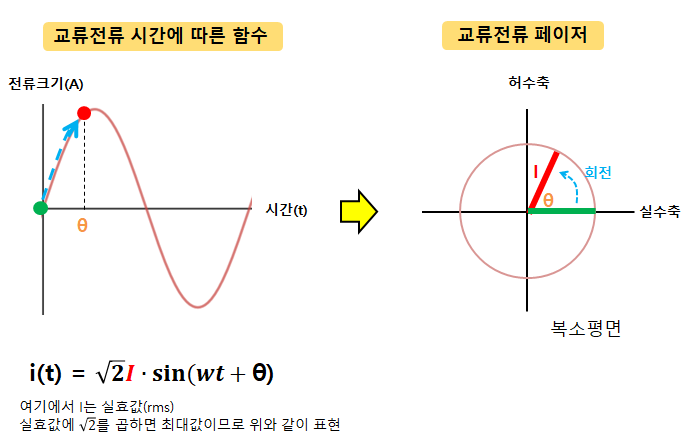
복소평면에서 x축은 실수축, y축은 허수축이다.
극좌표로 변환할 때는 시간에 따른 교류전류 함수i(t) = √2· I · sin(wt + θ) 에서의 실효값인 I를 가져와야한다.
페이저에서는 I의 일정한 크기를 가진 막대기가 원의 중심을 기준으로 시간에 따라 회전하면서 θ의 크기만 바뀌는 모양이다.
최초 왼쪽 그래프의 왼쪽 녹색 점은 오른쪽 복소평면에서 녹색 막대기와 같다.
왼쪽 그래프에서 시간이 흘러 교류전류가 빨간점에 위치하면 오른쪽 복소평면에서 빨간색 막대기와 같다.
이렇게 왼쪽 그래프에서 시간에 따라 한 주기를 움직이는 동안 오른쪽 복소평면에서 막대기는 한 바퀴를 돌게 된다.
이때 페이저는 두 가지 표현 방법으로 표현할 수 있다.
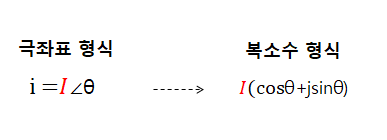
(1) 극좌표 형식
(2) 복소수 형식
(1) 극좌표 형식으로 교류전류 표현
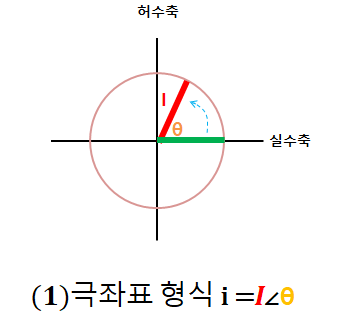
교류전류 i = I∠θ 이다.
일정한 크기의 실효값(I) 에 변하는 위상(θ)이 곱해진 형태로 표현한다.
(2) 복소수 형식으로 교류전류 표현

교류전류 i = Icosθ + Ijsinθ
크기가 I인 막대기가 θ만큼 움직였을 때 위치를 삼각함수를 이용하면 복소수 형식으로 표현할 수 있다.
이렇게 페이저는 극좌표 형식(∠θ)으로 표현할 수도 있고 복소수 형식(a+jb)으로 표현할 수도 있다.
실질적으로 우리가 계산을 쉽게 하기 위해 필요한 건 극좌표 형식이다. 크기와 위상으로만 표현되어 있기 때문에 계산이 편리하다.
그래서 복소수 형태가 아닌 극좌표 형식으로 변환해서 사용하면 된다.
복소수 형식으로 표현된 식도 공학용 계산기를 이용하면 쉽게 극좌표 형식으로 바꿀 수 있다.
계산기로 (복소수 -> 극좌표), (극좌표 -> 복소수)로 쉽게 바꿀수 있지만 기본적으로 바꾸는 식을 알고 있으면 도움이 된다.
바꾸는 식은 아래와 같다.
(극좌표 -> 복소수)
(복소수 -> 극좌표)

2. 교류식을 페이저로 변환하기 예시
두 교류 전류가 있다고 했을 때
이 교류 전류를 페이저식(극좌표 형식)으로 바꿔보자.
교류전류
1. i1 = 5√2 sin(wt - 60˚)
2. i2 = 5√2 sin(wt + 30˚)
1.
i1= 5√2 sin(wt - 60˚) 을 극좌표형식의 페이저로 변환하면
5√2는 최대값이므로 √2로 나눠줘야 실효값이 된다.
그러므로 실효값(I) = 5 이다.
위상(θ)는 -60을 그대로 가져오면 된다.
그러면 i1의 페이저식 = 5∠-60˚ 이다.
2.
i2 = 5√2 sin(wt + 30˚)를 극좌표형식의 페이저로 변환하면
5√2는 최대값이므로 √2로 나눠줘야 실효값이 된다.
그러므로 실효값(I) = 5 이다.
위상(θ)는 30을 그대로 가져오면 된다.
그러면 i2의 페이저식 = 5∠30˚ 이다.
3. 페이저식의 더하기, 빼기, 곱하기, 나누기 예시
만약
i1 = 5√2 sin(wt - 60˚)
i2 = 5√2 sin(wt + 30˚)
위의 시간에 따른 교류전류 함수를 곱하거나 더하거나 빼려면 아주 복잡한 과정을 거쳐야한다.
그러나 페이저를 이용해 변환하면 아래와 같이 계산이 간단해진다.
I1 = 5∠-60˚
I2 = 5∠30˚
위에서 구한 두 교류전류의 페이저식을 이용해 계산해보자.
(1) 곱하기 (I1 × I2)
5∠-60˚ × 5∠30˚
위처럼 실효값 크기가 같은 두 페이저식의 곱은 실효값끼리는 곱하고 위상값끼리는 더해주면 된다.
5x5 ∠(-60˚+30˚)
= 25∠-30˚
(2) 나누기 (I1 ÷ I2)
5∠-60˚ ÷ 5∠30˚
실효값 크기가 같은 두 페이저식의 나누기는 실효값끼리는 나누고 위상값끼리는 빼주면 된다.
5÷5 ∠(-60˚-30˚)
= 1∠-90˚
(3) 더하기, 빼기 (I1 + I2), (I1 - I2)
5∠-60˚ + 5∠30˚ , 5∠-60˚ - 5∠30˚
더하기나 빼기의 경우 공학용 계산기를 이용해야 계산이 빠르다. 위의 값을 그대로 입력해서 구하면 계산기에 복소수형태(a+jb)가 나온다. 이걸 계산기의 변환 버튼을 이용하면 다시 극좌표 형태로 바꿀 수 있다.
다만 극좌표를 이용하면 두 식의 더하기, 빼기의 값의 크기와 위상을 대략적으로 알 수 있다는 장점이 있다.
더하기를 예로 들어보자.
5∠-60˚ , 5∠30˚ 를 복소평면 위에 그려보면 아래처럼 쉽게 그릴 수 있다.
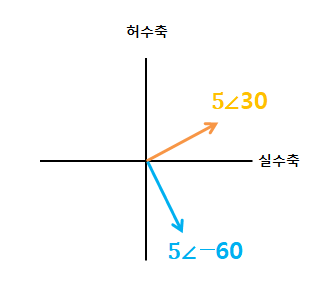
둘의 합을 그려보는 것도 어렵지 않다.
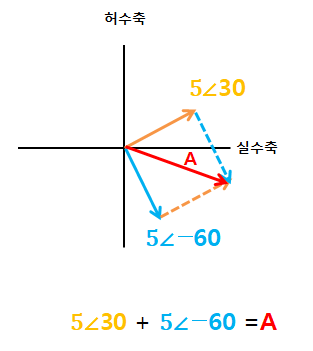
둘의 합은 A인데 이 그림만 보고도 둘의 합이 커지겠구나, 위상은 어느정도 되겠구나 짐작할 수 있다.
이런 점 때문에 실무에서 유용하게 쓰일 수 있다.
'전기공부 > 전기회로' 카테고리의 다른 글
| 8. 전압,전류 페이저도 그리기(순인덕터부하) (0) | 2020.11.17 |
|---|---|
| 7. 전압,전류 페이저도 그리기(순저항부하) (0) | 2020.11.09 |
| 5. 전압원과 전류원에 대해 알아보자.(2)전류원 (1) | 2020.11.01 |
| 4. 전압원과 전류원에 대해 알아보자.(1)전압원 (0) | 2020.10.31 |
| 3. 교류 전류 표현 이해 (최대값, 평균값, 실효값) (0) | 2020.10.26 |