2020. 9. 17. 20:29ㆍ전기공부/전자기학
7. 도체에 전류가 흐를 때 자기력의 크기와 방향에 대해 알아보자(1)
전류가 흐를 때 주변에 나침반을 두면 나침반이 회전한다.
전류가 흐르면 주변에 어떠한 힘이 발생해서 나침반에 영향을 준 것이다.
여기서 나침반에 영향을 준 힘은 '자기력'이다. (자기력이 영향을 미치는 공간 = 자기장)
앞에서 전류와 자기장의 관계에 대해 알아보았다.
전류가 발생하면 자기장이 생기고, 자기장이 발생하면 전류가 생겼다. 전류와 자기장은 서로의 원인이자 결과였다. 둘은 차원이 다르지만 항상 같이 존재했다.
이번에는 도체에 전류가 흐를 때 자기력의 크기와 방향에 대해 알아보자.
1. 도체에 작용하는 자기력의 크기 이해
2. 외적으로 자기력 방향을 알 수 있다.
3. 두 도체가 있을 때 자기력의 방향 확인
1. 도체에 작용하는 자기력의 크기 이해
도체에 작용하는 자기력의 크기에 대해 알아보자.
자세히 수학적으로 들어가기보다는 큰 흐름만 이해해보자.
도체에 작용하는 자기력의 크기 F = J X B 로 표현할 수 있다. ( J = 전류밀도, B = 자속밀도, X-외적)
전류밀도와 자기장의 외적이 도체에 작용하는 자기력의 크기이다.

여기서 자기력의 크기 F의 단위는 [N/m]이다.
말로 풀면 단위길이(m)당 작용하는 힘(N)이다.
전류밀도 J의 단위는 [A/m^2]이다.
단위면적(m^2)당 전류(A)이다.
자속밀도 B의 단위는 [wb/m^2]이다. ( [wb/m^2]는 우리가 잘 알고 있는 [T] - 테슬라와 같다.)
단위면적(m^2)당 자기력선의 수[mb]이다.
F[N/m] = J[A/m^2] X B[T]
이므로 양변에 m(미터)를 곱하면
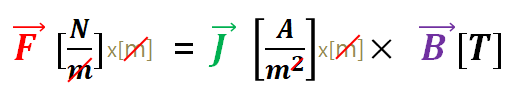
F[N] = J[A/m] X B[T] 가 된다.
그러므로 F[N]은 그냥 힘이고, J는 단위길이(m)당 전류가 된다.
ex) 자계 내에 전류가 흐르는 L(m) 직선도체가 있을 때 이 도체에 작용하는 힘
자기력 F[N] = J[A/m] X B[T] 이므로
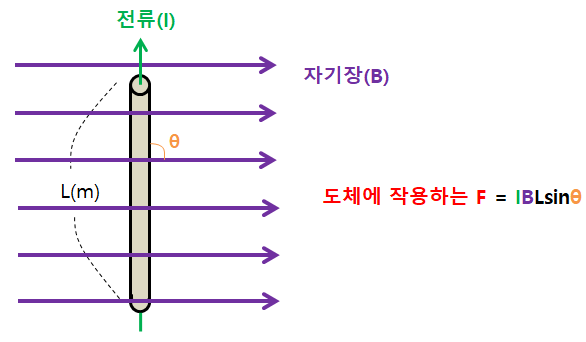
F = 전류(I) x 도선의 총길이(L) x B x sinθ 가 된다. ( 벡터에서 곱으로 바뀌면서 외적(X)는 sinθ로 바뀐다.)
그래서 도체에 작용하는 힘은 많이 사용하는 공식인 F = IBLsinθ 가 된다.
ex) 두 도체(A,B)가 r(m)만큼 떨어져 있을 때 B도체에 작용하는 자기력의 크기
두 도체가 나란히 있을 때 암페어 오른나사 법칙을 이용하면 자기장의 방향은 전류와 90º이다.
F = IBLsinθ에서 θ에 90º를 넣으면 F = IBL이고 단위길이당 F = IB이다.
직선도체이므로 암페어 법칙을 적용하면 (암페어 법칙은 따로 정리가 필요)
H =I/2πr 이다.
B= μH이므로 H에 위의 값을 넣으면 B=μI/2πr이더,
자기력 F = IB에 B=μI/2πr 을 넣으면
두 도체 사이에 작용하는 자기력의 크기 F = (μ x i^2) / 2πr 이다.

i^2이외에는 모두 상수이므로
두 도체 사이에 작용하는 자기력 F는 전류 i의 제곱에 비례함을 알 수 있다.
F ∝ i^2
우리가 다루는 전력시스템은 '전압원 시스템'이다. 이 말은 전압을 일정하게 유지하는 시스템이라는 말이다.
다만 전압원에 부하가 얼마나 걸리느냐에 따라서 전류값이 바뀐다.
그런 면에서 자기력(F)이 전류(i)의 제곱에 비례한다는 관계는 굉장히 중요하다.
전류의 제곱에 비례하므로 자기력은 전류에 아주 민감하게 반응한다.
자기력이 모터를 돌리는 힘으로 작용할 경우에는 긍정적인 에너지로 쓰이지만
필요치 않은 곳에서 자기력이 강하게 발생할 경우 설비에 큰 손상을 줄 가능성이 있다.
그래서 자기력과 전류의 관계를 잘 이해하고 있는 게 중요하다.
'전기공부 > 전자기학' 카테고리의 다른 글
| 9. 기계력(자기력)이 위험한 이유 (0) | 2020.09.25 |
|---|---|
| 8. 도체에 전류가 흐를 때 자기력의 크기와 방향에 대해 알아보자(2) (0) | 2020.09.18 |
| 6. 전류와 자기장의 관계 (0) | 2020.09.16 |
| 5. 커패시터의 전압, 전류 그래프 확인 (0) | 2020.09.15 |
| 4. '유전체'의 역할(커패시터 원리) (0) | 2020.09.10 |